[ad_1]
The Tree-3 architecture and initial weights
The Tree-3 architecture (Fig. 1c) consists of M = 16 branches. The first layer of each branch consists of K (6 or 15) filters of size (5 × 5) for each one of the three RGB channels. Each channel is convolved with its own set of K filters, resulting in 3 × K different filters. The convolutional layer filters are identical among the M branches. The first layer terminates with a max-pooling consisting of (2 × 2) non-overlapped squares. The second layer consists of a tree sampling. For the CIFAR-10 dataset, this layer connects hidden units from the first layer using non-overlapping rectangles of size (2 × 2 × 7), two consecutive rows of the 14 × 14 square, without shared-weights, but with summation over the depth of K filters, yielding an output of (16 × 3 × 7) hidden units. The third layer fully connects the (16 × 3 × 7) hidden units of the second layer with the 10 output units, representing the 10 different labels. For the MNIST dataset, the input is (28 × 28) and after the (5 × 5) convolution the output of each filter is (24 × 24) which terminates as (12 × 12) hidden units after performing the max-pooling. The tree sampling layer connects hidden units from the first layer using non-overlapping rectangles of size (4 × 4 × 3), without shared-weights, but with summation over the depth of K filters, resulting in a layer of (16 × 3) hidden units. The third layer fully connects the (16 × 3) hidden units of the second layer with the 10 output units, representing the 10 different labels. For online learning, the ReLU activation function is used, whereas Sigmoid is used for offline learning, except for K = 15, M = 80, where the ReLU activation function is used. All weights are initialized using a Gaussian distribution with zero mean and standard deviation according to He normal initialization26.
Details of the weight, input, and output sizes for each layer of the Tree-3 architecture are summarized below.
| Type | Weight size | Input size | Output size |
|---|---|---|---|
| Conv2d | \(3\mathrm x \mathrmK x 5\mathrm x 5\) groups = 3 | \(3\mathrm x 32\mathrm x 32\) | \(3\mathrmK x 28\mathrm x 28\) |
| MaxPool2d | \(2\mathrm x 2\) | \(3\mathrmK x 28\mathrm x 28\) | \(3\mathrmK x 14\mathrm x 14\) |
| Tree Sampling | \(3\mathrmK x M x 14\mathrm x 14\) | \(3\mathrmK x 14\mathrm x 14\) | \(3\mathrmM x 7\) |
| FC | \(21\mathrmM x 10\) | \(3\mathrmM x 7\) | \(10\) |
Data preprocessing
Each input pixel of an image is divided by the maximal value for a pixel, 255, and next multiplied by 2 and subtracted by 1, such that its range is [− 1, 1]. The performance was enhanced by using simple data augmentation derived from original images, such as flipping and translation of up to two pixels for each direction. For offline learning with K = 15 and M = 80, the translation was up to four pixels for each direction.
Optimization
The cross-entropy cost function was selected for the classification task and was minimized using the stochastic gradient descent algorithm. The maximal accuracy was determined by searching over the hyper-parameters, i.e., learning rate, momentum constant and weight decay. Cross validation was confirmed using several validation databases each consisting of 10,000 random examples as in the test set. The averaged results were within the standard deviation (Std) of the reported average success rates. Nesterov momentum27 and L2 regularization method28 were used.
Number of paths: LeNet-5
The number of different routes between a weight emerging from the input image to the first hidden layer and a single output unit is calculated as follows (Fig. 1b). Consider an output-hidden unit of the first hidden layer, belonging to one of the (14 × 14) output hidden units of a filter at a given branch. This hidden unit contributes to a maximum of 25 different convolutional operations for each filter at the second convolutional layer. The output of this layer results in 16 × 25 different routes. The max-pooling of the second layer reduces the number of different routes to 16 × 25/4 = 100. Each of these routes splits to 120 in the third fully connected layer and splits again to 84 in the fourth fully connected layer. Hence, the total number of routes is 100 × 120 × 84 = 1,008,000 different routes.
Hyper-parameters for offline learning (Table 1, upper panel)
The hyper-parameters η (learning rate), μ (momentum constant27) and α (regularization L228), were optimized for offline learning with 200 epochs. For LeNet-5, using mini-batch size of 100, η = 0.1, μ = 0.9 and α = 1e−4. For Tree-3 (K = 6 or 15, M = 16 or M = 80), using mini-batch size of 100, η = 0.075, μ = 0.965 and α = 5e−5 and for 10 Tree-3 (K = 15, M = 80) architectures where each one has one output only, using mini-batch size of 100, η = 0.05, μ = 0.97 and α = 5e−5. The learning-rate scheduler for LeNet-5, η = 0.01, 0.005, 0.001 for epochs = [0, 100), [100, 150), [150, 200], respectively. For Tree-3 (K = 6, M = 16) η = 0.075, 0.05, 0.01, 0.005, 0.001, 0.0001) for epochs = [0, 50), [50, 70), [70, 100), [100, 150), [150, 175), [175,200], respectively. For Tree-3 (K = 15, M = 16) η = 0.075, 0.05, 0.01, 0.0075, 0.003 for epochs = [0, 50), [50, 70), [70, 100), [100, 150), [150,200], respectively. For Tree-3 (K = 15, M = 80) and 10 Tree-3 (K = 15, M = 80), η decays by a factor of 0.6 every 20 epochs. For Tree-3, the weight decay constant changes after epoch 50 to 1e−5. For the MNIST dataset the optimized hyper-parameters were a mini-batch size of 100, η = 0.1, μ = 0.9 and α = 5e−4. The learning rate scheduler was the same as for Tree-3 (K = 15, M = 16), on the CIFAR-10 dataset.
Hyper-parameters for online learning (Table 1, bottom panel)
The hyper-parameters mini-batch size, η (learning rate), μ (momentum constant27) and α (regularization L228), were optimized for online learning using the following three different dataset sizes (50k, 25k, 12.5k) examples. For LeNet-5, using mini-batch sizes of (100, 100, 50), η = (0.012, 0.017, 0.012), μ = (0.96, 0.96, 0.94) and α = (1e−4, 3e−3, 8e−3), respectively. For Tree-3 (K = 6, M = 16), using mini-batch sizes of (100, 100, 50), η = (0.02, 0.03, 0.02), μ = (0.965, 0.965, 0.965) and α = (5e−7, 5e−6, 5e−5), respectively.
Ten Tree-3 architectures
Each Tree-3 architecture has only one output unit representing a class. The ten architectures have a common convolution layer and are trained in parallel, where eventually the softmax function is applied on the output of the ten different architectures.
Pruned BP
The gradient of a weight emerging from an input unit connected an output via a single route (Tree-3 architecture, Fig. 1c), with non-zero ReLU activation function, is given by \(\Delta \left(W^Conv\right)=Input\cdot W^Tree\cdot W^FC\cdot (Output-Output_desired)\), otherwise, its value is equal to zero.
Statistics
Statistics of the average success rates and their standard deviations for online and offline learning simulations were obtained using 20 samples. The statistics of the percentage of zero gradients and their standard deviations in Fig. 2 were obtained using 10 different samples each trained over 200 epochs.
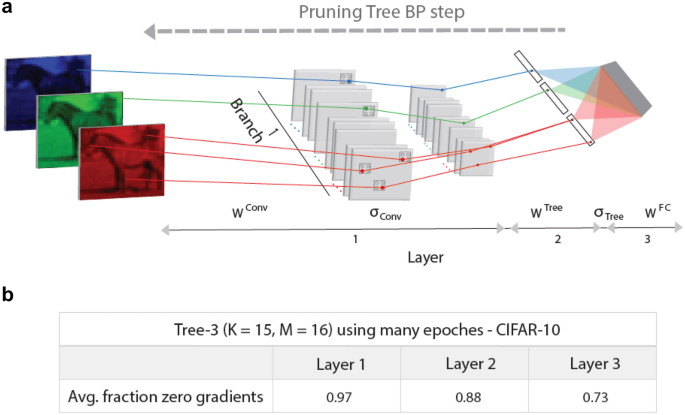
BP step on highly pruning Tree-3 architecture. (a) Scheme of a BP step in the first branch of a highly pruning Tree-3 architecture (Fig. 1d). The gray squares in the first layer represent convolutional hidden units, \(\sigma _Conv\), and max-pooling hidden units that are equal zero, except several denoted by RGB dots. The non-zero tree output hidden units, \(\sigma _Tree\), are denoted by black dots. The updated weights with nonzero gradients, in first layer, \(W^Conv\), second layer, \(W^Tree\), and third fully connected layer, \(W^FC\), are denoted by RGB lines. (b) Fraction of zero gradients, averaged over the test set, and their standard deviations for the tree layers of Tree-3 architecture (K = 15, M = 16), after many epochs (“Methods” section).
Hardware and software
We used Google Colab Pro and its available GPUs. We used Pytorch for all the programming processes.
[ad_2]
Source link